3.6 Logiska funktioner

Logiska funktioner används för att pröva olika situationer och agera olika beroende på omständigheter. Säg till exempel att en lärare vill sätta betyg på en elev beroende på elevens resultat på ett prov. Då är det lämpligt att använda en funktion som kan pröva om resultatet är över en viss nivå och i så fall sätta ett visst betyg. Vi skall i detta kapitel titta på hur sådana jämförelser görs och vilka logiska funktioner som finns.

3.6.1 Jämförelseoperatorer

Jämförelser är grundläggande i logiska tester. Det handlar helt enkelt om att se om värden är över eller under en viss nivå, om de är lika ett annat värde eller skiljt från ett annat värde. Till vår hjälp har vi då så kallade logiska operatorer. Dessa är hämtade från matematiken och ganska lätta att lära sig. De används sedan i olika logiska funktioner.

=	Är lika med
>	Är större än
<	Är mindre än
>=	Är större än eller lika med
<=	Är mindre än eller lika med
<>	Är inte lika med, är skiljt från

Jämförelseoperatorerna kan endast användas för att jämföra två värden med varandra. Vill vi jämföra fler värden samtidigt måste vi använda så kallade logiska operatorer. (Se kap. 3.6.5).

3.6.2 Om() (eng. If)

Vi skall nu använda funktionen IF() för att sätta betyg på studenter på ett prov. De som har fått mer än 20 poäng skall få godkänt. Övriga skall få underkänt. Funktionen har följande argument:

IF(logisk_prövning; värde_om_sant; [värde_om_falskt])

I vårt fall är värdena som skall skrivas ut texter, betygen "G" och "U". Därför måste vi omge dessa värden med citationstecken i vår kod. Om det vi vill skriva ut istället är tal så skall citationstecken inte användas.

Till vår hjälp gör vi en jämförelse där vi ser om värdet i kolumnen över resultatet på provet är större än 20. Om denna prövning visar sig stämma så blir "G" resultatet av funktionen (värde om sant) annars blir det "U" (värde om falskt). (Se figur 37)

Figur 37. Betyg sätts (FunctionOm01.xlsx)

I exemplet Funktion_Om01.xlsx får inte Drusilla godkänt. Vi skall ändra det så att alla som har 20 poäng eller mer får godkänt på kursen. Vi korrigerar då if-satsen till:

IF(C3>=20; "G"; "U")

Notera att i vårt exempel jämför vi om resultatet på tentamen är över ett visst värde. Det är med andra ord två tal som vi jämför med varandra. Det går även att jämföra två texter. I så fall måste texter i jämförelsen omges med citationstecken. Vill vi till exempel granska om det står "Kalle" i A3 så måste namnet omges med citationstecken:

IF(A3="Kalle"; "Namnet är funnet!"; "Namnet är inte funnet!")

3.6.3 OmFel() (eng. IfError)

Funktionen IFERROR är en mycket användbar funktion. Den används för att returnerna någon form av bättre felmeddelande om en beräkning har blivit felaktig. Funktionen har följande argument:

IFERROR(beräkning; värde_om_fel)

Den beräkning som utförs kan vara vilken beräkning som helst eller en annan funktion. Om en funktion läggs i en annan funktion så skall den inre funktionens namn inte föregås av ett =-tecken. (Se kap. 3.6.3). Värdet om fel kan vara ett felmeddelande, men även en helt annan beräkning. Om eventuellt önskat felmeddelande är en text skall den omges av citationstecken. Anropet nedan ger felmeddelande om värdet i A1 är noll:

IFERROR(5/A1; "kan inte dividera med noll")

3.6.4 Flera logiska tester nästlade

I kap. 3.6.2 satte vi betygen G och U beroende på resultat på ett prov. Verkligheten är dock inte alltid så enkel att det bara finns två alternativa värden. Tvärtom är det vanligt att betyg sätts i flera olika steg.

Vi skall nu se på ett exempel där 20 eller mer är godkänt och 25 eller mer är väl godkänt. Vår mänskliga hjärna kan direkt se vilket betyg en person skall ha om det bara finns några få poänggränser. En dator behöver dock pröva steg för steg. Sådan prövning görs med fördel från en extrem. Till exempel kan vi utgå från extremen om studenten har VG och i så fall sätta VG, i annat fall sätter vi ? som betyg. I nästa steg granskar vi om studenten når upp till G eller skall ha U. Till sist lägger vi samman dem genom att byta ut frågetecknet i den första granskningen mot hela den andra granskningen.

Vi skall ta det steg för steg men visar den färdiga lösningen redan nu i figur 38 för att det lättare skall framgår vad slutmålet är.

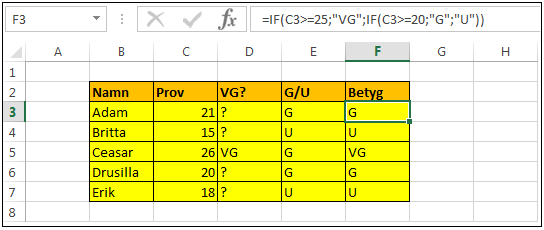
Figur 38. Nästlade villkor (Funktion_om02.xlsx) Första steget, i kolumn D, är att granska om studenten skall ha VG:

(C3>=25;"VG";"?")

Nästa steg är att i kolumn E granska om studenten har nått G eller skall ha U. Att Ceasar får såväl G som VG är inget problem eftersom vi utgår från extremen. Han kommer att få sitt VG och testen om han skall få G utförs aldrig i praktiken i F-kolumnen:

IF(C3>=20;"G";"U")

Det sista momentetn är att lägga samman de två föregående funktionerna. Det gör vi genom flera olika steg. Dessa steg använder sig av klipp och klistra. Vi gör så här

1. markera cellen D3

2. markera hela formeln i formelfältet med musen

3. tryck [Ctrl] + [C] för att kopiera allt

4. tryck [Esc] för att komma ur formelfältets redigeringsläge

5. markera F3 och klicka [Ctrl] + [V]. Formeln kopieras nu över som text och inga referenser räknas upp!

6. Markera E3

7. Markera i formelfältet hela formeln utom =-tecknet

8. Markera F3.

9. Sök i formelfältet upp texten "?" och sudda bort dessa tre tecken.

10. Tryck [Ctrl] + [V] på den plats där "?" fanns.

11. Tryck på [Enter]

Genom de elva stegen ovan tar vi de två fungerande funktionerna i D och E kolumnen och nästlar dem samman i F-kolumnen.

Erfarenhetsmässigt från kurser i Excel är det mycket vanligt att mpmentet 4 glöms bort, att vi glömmer trycka på [Esc]. Excel kommer att tolka det som att vi håller på att redigera formeln, vilket blir alldeles fel.

3.6.5 Logiska operatorer Och() (eng. And), Eller() (eng. Or) samt Icke() (eng. Not)

Ibland är det mer än ett villkor som skall vara uppfyllt för att vi skall vilja få ett visst resultat. Vi kan lösa det genom nästlade if-satser. Till exempel kan det vara så att en student skall ha godkänt på uppsatsen och på provet för att få godkänt på kursen. Vi kan då granska nästlat först om uppsatsen är klar och i så fall vilket betyget blir på basis av provet. Nackdelen med det är att nästling inte alltid är det kortaste sättet att skriva.

Till vår hjälp finns istället logiska operatorer som hjälper oss att granska flera saker samtidigt. De främsta av dessa är AND(), OR samt NOT().

Vi skall börja med att se på den förstnämnda och sätta betyg på en student om studenten har godkänt på uppsatsen och på tentamen. Tentamen har vi i figur 39 betygsatt med G eller U. För att studenten skall ha godkänt på kursen är det två villkor som skall vara uppfyllda:

C3="G"

D3>=20

Dessa två villkor, som båda skall vara sanna samtidigt, kan vi granska på en gång med hjälp av AND(). Dess argument är upp till 255 logiska tester:

AND(logisk_test1; [logisk_test2]; [...])

Vi stoppar nu in våra två villkor i funktionen AND(:

AND(C3="G"; D3>=20)

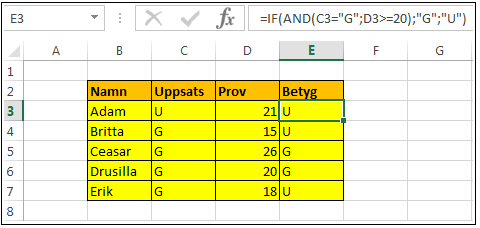
Figur 39. Logisk operator (Funktion_Om03.xlsx)

Den logiska testen kommer att returnera värdet sant eller falskt. Skriver vi vår AND-funktion i en cell kommer den även att visa värdet Sant eller Falskt. Nu används denna funktion i praktiken nästan alltid tillsammans med en annan funktion som granskar logiska tester. Vi stoppar helt enkelt in denna funktion i vår AND-funktion:

IF(AND(C3="G"; D3>=20); "G"; "U")

Funktionen OR kan även den granska upp till 255 värden för att se om de är sanna. Dess argument är:

OR(logisk_test1; [logisk_test2]; [...])

Skillnaden mellan de två funktionerna är att AND() returnerar sant endast om samtliga granskade värden är sanna. För OR räcker det att minst ett av de granskade värdena är sanna så returnerar den sant.

Till sist skall vi ta upp funktionen NOT(). Den vänder sant till falskt och falskt till sant. NOT(sant) blir följaktligen falskt. Funktionens kan granska alla logiska tester, till exempel med jämförelseoperatorer. Dess argument är:

NOT((logisk_test)